Magnetism and superconductivity do not usually get along very well – a superconductor always tries to keep an external magnetic field out of its interior. When this is not possible because the magnetic field is too strong, in Type II superconductors so called flux lines are formed – thin channels through which the magnetic field can pass through the superconductor keeping the rest of the material field free. Usually, these flux lines tend to form regular patterns. Now, two physicists from the Paul Scherrer Institute and the University of Birmingham in the UK have shown that such a pattern must depend on the direction of the external magnetic field. I. e., it is not possible that this pattern remains always the same when the superconductor is turned in a magnetic field. Thus, either there are different patterns for different directions of the magnetic field or the flux lines are arranged in an irregular way for particular directions of the field. These results are based on a mathematical principle known as the “Hairy ball theorem”.
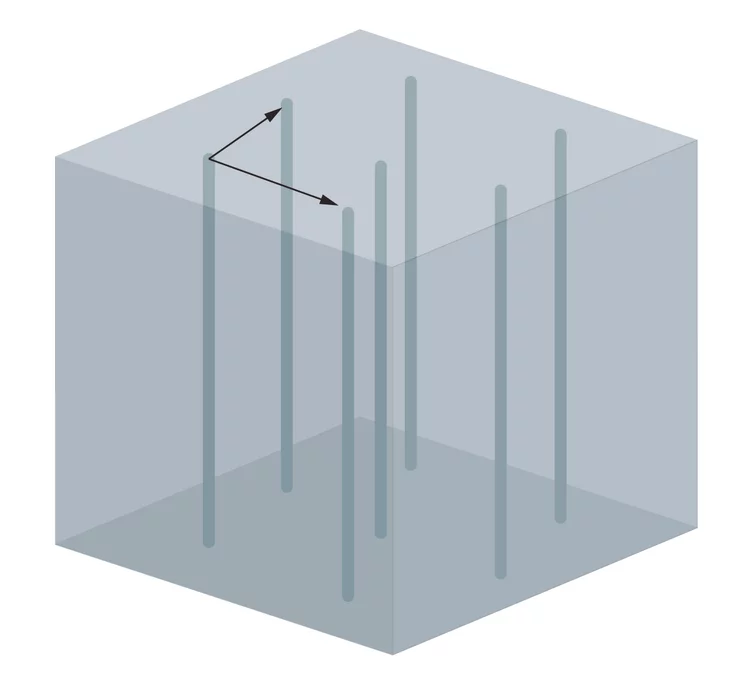
The flux lines
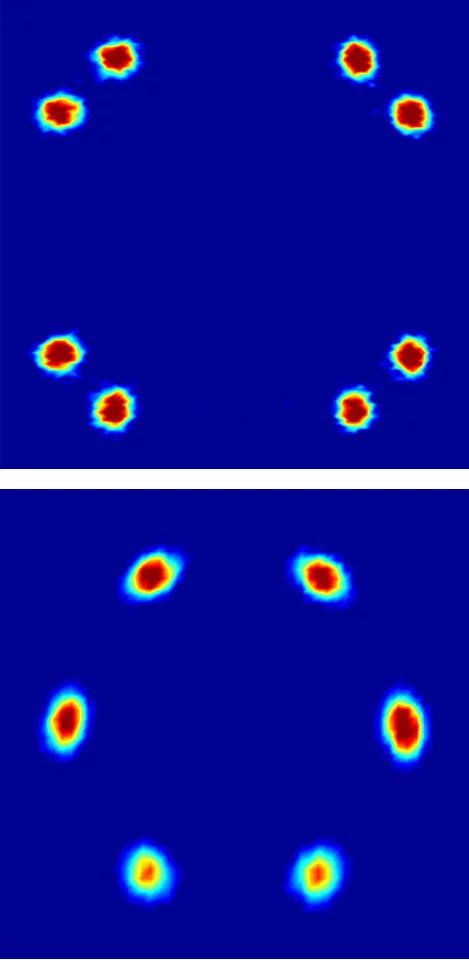
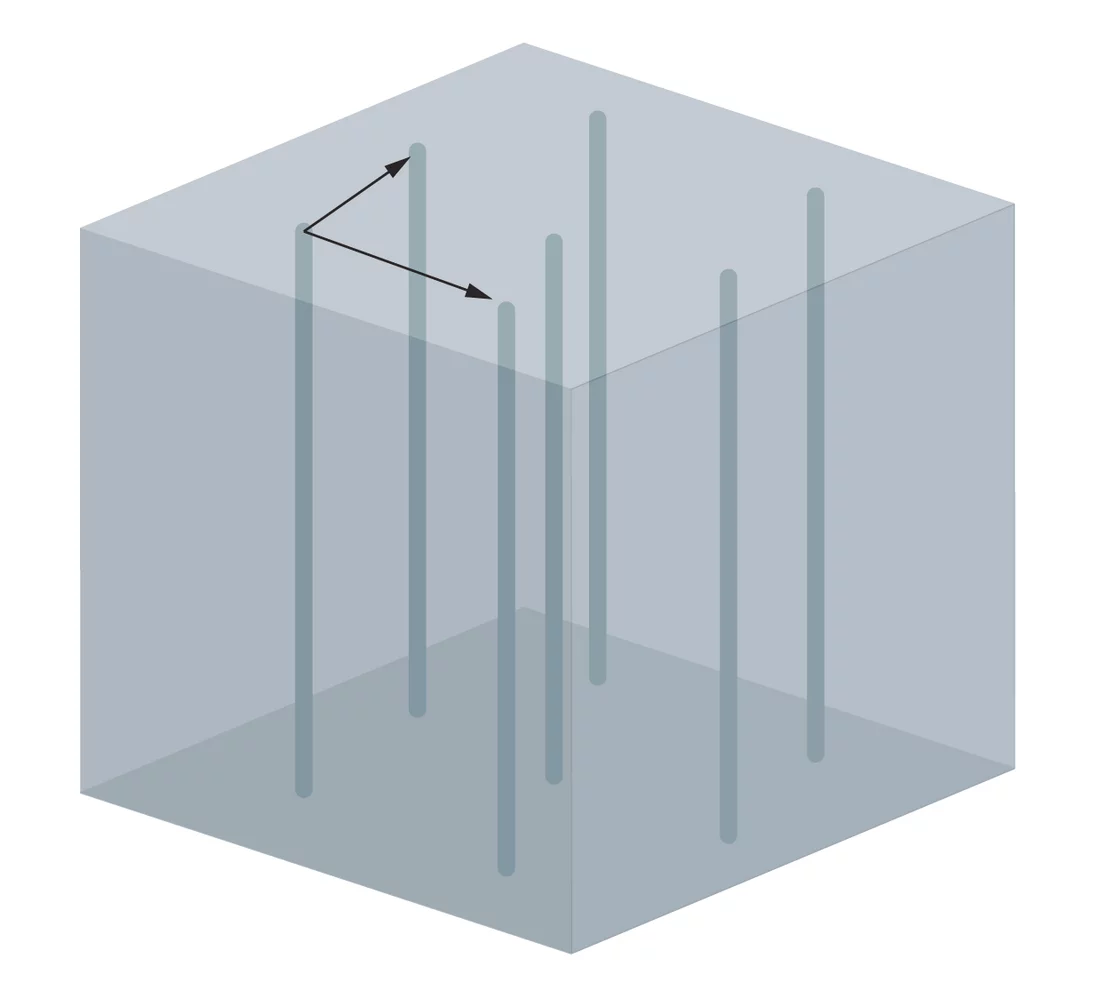
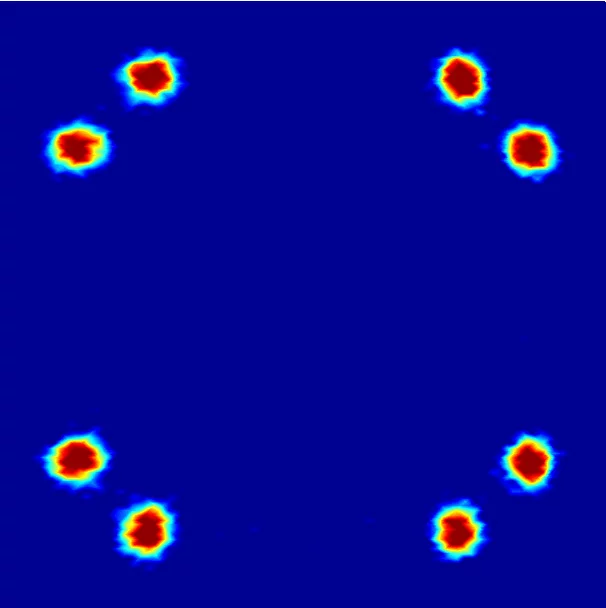
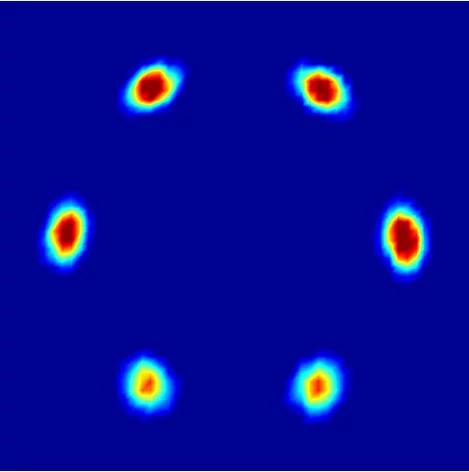
Superconductors are mostly known for their property that they conduct electric currents with no resistance at all. Another important property, however, is that they do not tolerate a magnetic field in their interior. When placed in a magnetic field, they guide the magnetic field on their outside and keep their interior free of magnetic fields. Type II superconductors – also known as high temperature superconductors – have a further option to protect themselves from magnetic fields. They can create so called flux lines that can guide the field through the superconductor. Inside the cores of the flux lines, the material is not superconducting anymore, but it remains superconducting anywhere else. In a sense, the material gives up superconductivity for a part of their interior in order to save it for all the rest. When the external field is made stronger, more flux lines are created – for a very strong field, superconductivity breaks down completely. The flux lines are always parallel to the magnetic field and usually order in regular patterns. The arrangement of the flux lines can be determined in neutron scattering experiments such as those performed at the neutron source SINQ at the Paul Scherrer Institute.
Different patterns for different directions
Already 30 years ago researchers in the US observed that the arrangement of the flux lines in superconducting niobium changes when the superconductor is rotated in the external magnetic field. Thus, their arrangement depends on the direction in which the magnetic field penetrates the superconductor. These investigations were taken up by several groups in the past years performing experiments on niobium and the results confirmed what had been observed before: when the sample was rotated in the magnetic field, the pattern of the flux lines changed suddenly or the pattern disappeared completely and the lines were arranged in an irregular way. Now, Mark Laver from the Paul Scherrer Institute and Edward M. Forgan from the University of Birmingham have shown that this is not a peculiarity of niobium but rather a general rule based on a mathematical law known as the “Hairy ball theorem”.
The “Hairy ball theorem”
“You can't comb a hairy ball flat without creating a cowlick” is a popular way of stating the contents of the “Hairy ball theorem”. All that with the additional assumption that the ball has to be combed in a continuous manner, i.e., hair at nearby points should point in similar directions. Dishevelled hair would not solve the problem. The theorem has far reaching consequences in many fields. For example, the theorem predicts that there is always at least one place on Earth where the wind is still. Here, the directions of the wind correspond to the hair of the hairy ball.
The idea
The following mathematical reasoning is behind the connection between the theorem and the flux lines. One can depict the external magnetic field that penetrates the superconductor by an arrow (a vector) with the direction of the arrow corresponding to the direction of the field and the length corresponding to strength of the field. In the experiment, the direction of the field is changed while its strength remains unchanged. Thus, these vectors always have the same length. If one now imagines that all these vectors start at the same point in space, all the ends of the arrows will lie on a sphere. This is the sphere (the surface of the ball) needed for the hairy ball theorem.
The flux lines in a superconductor are always parallel to the external magnetic field. Whenever they are arranged in a regular pattern, one can describe this pattern using two arrows or vectors. To do so, one can pick an arbitrary flux line and consider a vector perpendicular to this flux line connecting it with one of the closest other flux lines. Although there are several such vectors, it is enough to consider two of them that are not parallel to each other to be able to recreate the whole structure. To do so, one simply has to start at one flux line, attach one of these vectors there and place a new flux line at the end of the vector. If you continue using both vectors, you get the pattern of the flux lines. These vectors defining the pattern of the flux lines are the hair needed for the hairy ball theorem – two of them at every spot.
If we now assume that the pattern of the flux lines remains the same for all directions of the magnetic field, one arrives at a contradiction. The assumption means that the vectors connecting the flux lines differ only slightly for nearby points on the sphere defined by the magnetic field vectors. But this is not possible according to the hairy ball theorem.
From a physical point of view, it is clear that the pattern need not remain unchanged as the different directions within the material are not equivalent. To see this, one has to take into account that the superconductor has a crystal lattice that defines preferred directions.
Various solutions
Nature solves this problem in a variety of ways. In one case, there are sharp jumps in the pattern as the direction of the magnetic field is changed. Another possibility is that the flux lines are arranged in an irregular way for some directions of the magnetic field. In these cases, there are no vectors that would determine this arrangement. The third possibility is that there are two patterns that penetrate each other.
“Boost comparable to the development of the CT scan”
"The hairy ball theorem makes it clear how important angle-resolved studies of the magnetic vortices in superconductors are. For superconductivity, this could represent a potential boost in our insight comparable to the development of the CT scan in medicine" is how Mark Laver estimates the relevance of his research.
Text: Paul Piwnicki
About PSI
The Paul Scherrer Institute develops, builds and operates large-scale, complex research facilities, and makes these facilities available to the national and international research community. The Institute”s own research focuses on solid-state physics and the materials sciences, elementary particle physics, biology and medicine, as well as research involving energy and the environment. With a workforce of 1400 and an annual budget of about 300 million CHF, PSI is the largest research institution in Switzerland.
Contacts
Mark Laver, Labor für Neutronenstreuung, Paul Scherrer Institut, 5232 Villigen PSI, Switzerland;Phone: +41 56 310 5420; E-mail: mark.laver@psi.ch [English, French]
Paul Piwnicki, Abteilung Kommunikation, Paul Scherrer Institut, 5232 Villigen PSI, Switzerland;
Phone: +41 56 310 29 40, E-mail: paul.piwnicki@psi.ch [German, English]
Orginal publication
Magnetic flux lines in type-II superconductors and the 'hairy ball' theoremMark Laver and Edward M. Forgan;
Nature Communications, 1 (27 July 2010)
DOI: 10.1038/ncomms1047