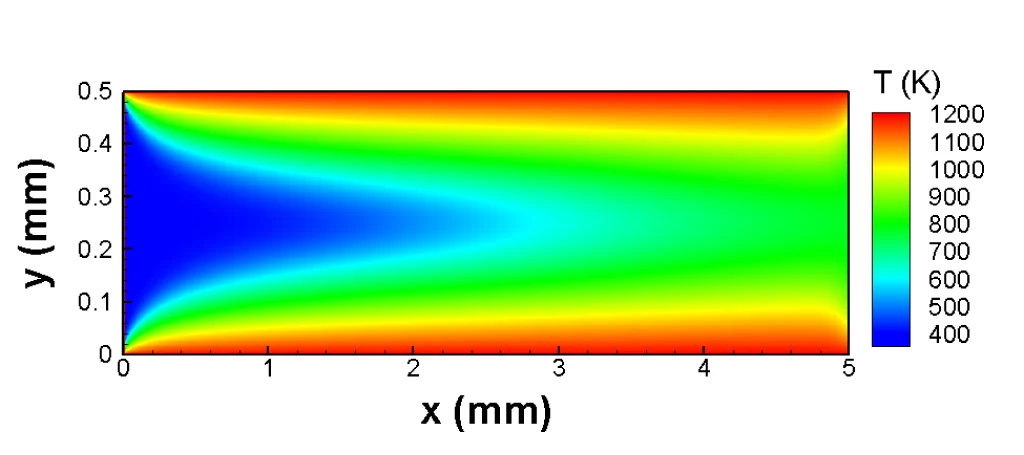
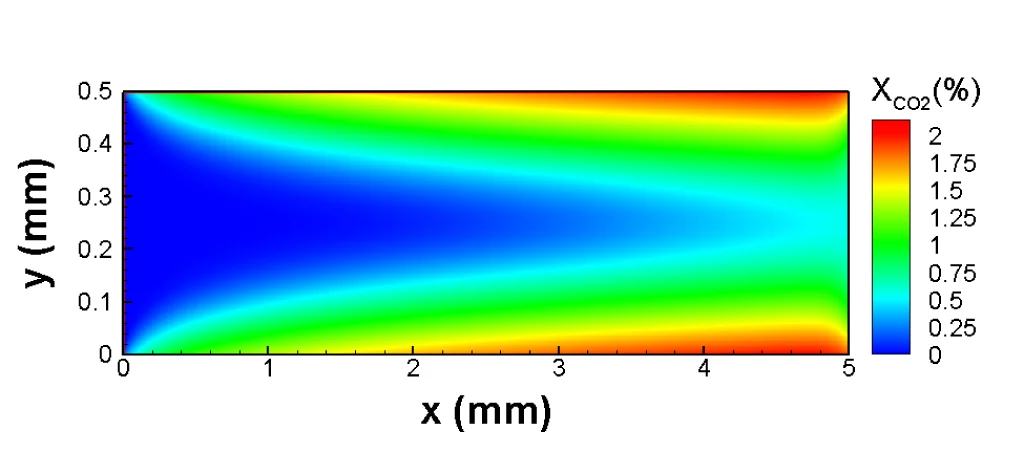
The Lattice-Boltzmann Method was developed in the early 1990s as a calculation approach to solve the Boltzmann equation numerically, i.e. with the aid of computers. The Austrian physicist Ludwig Boltzmann formulated the equation that would eventually be named after him in 1867, thereby establishing the kinetic theory of gases that is successful to this day in describing the properties of ideal gases, such as temperature and pressure, a result of the motion and collision of atoms or molecules. Researchers from the Paul Scherrer Institute (PSI) have now extended the Lattice-Boltzmann Method’s field of application with a new model that is able to describe more complex processes.
Although the Boltzmann equation has ever since been used by physicists to describe the behavior of gases, a universal, exact, mathematical solution to the equation is impossible to find.Lacking a solution that can be written down with a pen and paper, the scientists only had one option left: computer calculations. The Lattice-Boltzmann Method tries to solve exactly this problem.
Divide and conquer
The Boltzmann equation is a successful attempt to describe complex gas dynamics in a statistical way. . In other words, instead of following every single molecule in its random movement, the probability of a certain number of molecules being within a certain spatial and velocity range is computed.
The Lattice-Boltzmann Method simplifies the problem further by using the art of discretisation, which means that instead of following the movement of the gas molecules in the entire space-filling continuum, you content yourself with knowing how certain groups of molecules behave at certain points. The space continuum is thus replaced by a lattice comprising these points, thereby reducing the computational effort required and eventually making a computer simulation possible.
You just have to know at any given time whether a group of molecules is on a particular lattice point and, if so, how quickly they are moving and in which specific direction. Then, the time evolution of the system takes place in two steps. First, all particle groups are jumping to the next lattice point depending on the direction they are moving in. Second, wherever groups of molecules meet each other, they collide and as a result their velocity and direction are altered.
The computation of large and complex setups is facilitated by the fact that a lattice point communicates and is influenced only by its neighboring lattice points. In other words, you create cells on the lattice in a way that the computations do not require information of the entire simulated space.. And this is precisely where a major advantage of the Lattice-Boltzmann Method lies: the calculations can proceed for the individual cells independently of one another and on many processors at once. This separation (parallelisation) greatly reduces the simulation time required depending on the number of processors available.
Efficient – even when things get tight
In a wide variety of situations, the Lattice-Boltzmann Method provides a good alternative to simulate flows. However, one of the method’s main advantages lie in its potential of describing micro-flows, which occur in small energy converters such as fuel cells for portable devices and in most technical catalysts, for instance. In such systems, gases or liquids have to move through a very tight space or microscopic pores. In these cases, the flow processes cannot be described using continuum physical description. Since the Lattice-Boltzmann Method is precisely based on a microscopic theory of flow processes, it has the capacity to describe flows at the microscale. Nonetheless, the method had a long way to go before reaching today’s versatility. “Twenty years ago, the possibilities that this simulation method offered were still very limited,” explains Ioannis Mantzaras, the head of the Combustion Fundamentals Group at the PSI. Using the pure Lattice-Boltzmann Method, i.e. without aid of other tools, virtually only ideal gases at a constant temperature could be described. However, most of the real-life applications involve the flow of mixtures in a variable temperature environement.
Increasingly more realistic simulations
The rapid development of computational power and the storage capacity of computers along with the improvement of calculation procedures (algorithms) and physical models in recent years, have increased tremendously the simulation possibilities. Today, using Lattice-Boltzmann models scientists are able to realisticially study highly complex systems on the computer with a reasonable amount of effort.
The PSI researchers have also benefited from this. For the first time, they have now developed a model that allows the accurate description of the flow of gas or liquid mixtures at a variable temperature environement using the Lattice-Boltzmann Method (e.g. combustion simulations). This involved overcoming a serious drawback in the existing mixture Lattice-Boltzmann models : their inability to describe accurately the universal law of energy conservation. The scientists achieved this by skilfully improving the mathematical description of the discretized collision processes among the gas molecules.
Understanding the underlying processes and reducing development costs
The PSI scientists’ work opens a window to more realistic computer simulations of many complex technical processes. “Gas mixtures with variable temperatures are present in a wide variety of technical systems, including most microporous structures of technical catalysts, diesel particle filters, combustion microreactors or fuel cells,” says Nikolaos Prasianakis, one of the developers of the model. “By simulating these systems on the computer and by understanding the underlying physics, we are currently able to reduce the future development costs,” he adds. “After all, you can run more scenarios on the computer than in real tests, where expensive prototypes require a significant manufacturing time and can be destroyed or damaged. Nowadays, for example, models of cars or airplanes are entering the wind tunnels only after their aerodynamic behavior has been thoroughly tested using computer simulations” Although experiments remain indispensable, simulations enable them to be planned and conducted more efficiently.
Extensive validation
Validation tests of every computational model are absolutely necessary , even if the mathematical description is sound and solid. Therefore, the PSI researchers extensively tested whether their model can indeed reproduce the correct behavior of the simulated flows. In doing so, they were able to demonstrate for example that their method describes accurately the changes in the speed of sound when the temperature of the gas medium changes. The model also shows excellent behavior in all cases where an exact mathematical solution is known. Finally, in more demanding benchmarks, they showed that their model produces results that coincide with those of other established simulation methods. In its now-published form, the model only applies to two-dimensional flows from a gas mixture comprising of two chemical substances. However, the researchers showed that the model can easily be extended to three dimensions and mixtures made of any desired number of components.
Text: Leonid Leiva
Contact
Dr. Ioannis Mantzaras, Head of the group Combustion Fundamentals, Paul Scherrer Institut,Telephone: +41 56 310 40 46, E-Mail: ioannis.mantzaras@psi.ch
Original Publications
Lattice Boltzmann model for thermal binary-mixture gas flowsJinfen Kang, Nikolaos I. Prasianakis, John Mantzaras
Physical Review E, 87, 053304, 2013.
DOI: 10.1103/PhysRevE.87.053304
Lattice Boltzmann model for the simulation of multicomponent mixtures
S. Arcidiacono, I.V. Karlin, J. Mantzaras, C. E. Frouzakis,
Physical Review E, 76, 046703, 2007.
DOI: 10.1103/PhysRevE.76.046703