Die Gitter-Boltzmann-Methode entstand Anfang der 1990er Jahre als eine Berechnungsmethode, um die Boltzmann-Gleichung numerisch, also mithilfe von Computern zu lösen. Der österreichische Physiker Ludwig Boltzmann hatte die nach ihm benannte Gleichung bereits im Jahr 1867 formuliert. Damit begründete er die bis heute gültige kinetische Gastheorie, mit der Eigenschaften von „idealen Gasen“ wie Temperatur und Druck als Ergebnis der Bewegungen und Kollisionen von Atomen oder Molekülen beschrieben werden. Forscher des Paul Scherrer Instituts PSI erweitern nun mit einem neuen Modell den Anwendungsbereich der Gitter-Boltzmann-Methode auf komplexere Situationen.
Obwohl die Boltzmann-Gleichung seit jeher von Physikern verwendet wird, um das Verhalten von Gasen zu beschreiben, ist es bis heute nicht gelungen, eine allgemein gültige, exakte mathematische Lösung dieser Gleichung zu finden. Mangels einer Lösung, die man mit Bleistift und Papier hinschreiben kann, blieb den Wissenschaftlern nur der Weg über Computerberechnungen übrig. Gerade aus dieser Not entstand die Gitter- Boltzmann-Methode.
Teile und herrsche
Die Boltzmann-Gleichung ist ein erfolgreicher Versuch, mit statistischen Aussagen, das äusserst komplexe „Innenleben“ eines Gases zu erfassen. Das heisst: statt jedes einzelne Molekül in seiner chaotischen Bewegung zu verfolgen, berechnet man die Wahrscheinlichkeit, dass eine bestimmte Anzahl Moleküle sich in einem gewissen Raum- und Geschwindigkeitsbereich befinden.
Die Gitter-Boltzmann-Methode vereinfacht das Problem zusätzlich durch den Kunstgriff der Diskretisierung. Das heisst: Statt die Bewegung der Gasmoleküle im gesamten raumausfüllenden Kontinuum zu verfolgen, begnügt man sich damit zu wissen, wie sich Moleküle an bestimmten Punkten und verhalten. Das Raum-Kontinuum wird also durch ein aus diesen Punkten bestehendes Gitter ersetzt; dadurch wird der Rechenaufwand reduziert.
Man muss nur noch zu jedem Zeitpunkt wissen, ob sich an einem bestimmten Gitterpunkt ein Molekül befindet und wenn ja, wie schnell und in welche Richtung sich dieses Molekül bewegt. Die zeitliche Entwicklung des Gaszustandes wird dann in jeweils zwei Schritten vollzogen. Erstens werden alle Moleküle gemäss ihrer Bewegungsrichtung zum nächsten Gitterpunkt verschoben. Zweitens wird dort, wo Moleküle aufeinander treffen, deren Kollision ausgeführt, wonach sich diese Moleküle in neue Richtungen und mit neuen Geschwindigkeiten bewegen.
Der Rechenaufwand wird noch einmal dadurch gesenkt, dass Veränderungen an einem Gitterpunkt nur durch den Einfluss der unmittelbar benachbarten Gitterpunkte zustande kommen. Das heisst, man bildet Zellen im Gitter, die vom Rest des Gitterraums isoliert sind. Und gerade darin liegt ein wichtiger Vorteil der Gitter-Boltzmann-Methode: die Berechnungen können für die einzelnen Zellen unabhängig von einander und gleichzeitig auf vielen Prozessoren ablaufen. Durch diese Aufteilung (Parallelisierung) verringert sich der Zeitaufwand je nach Anzahl verfügbarer Prozessoren stark.
Effizient, auch wenn es eng wird
Die Gitter-Boltzmann-Methode liefert in einer Vielzahl von Situationen eine gute Alternative zu etablierten Strömungssimulationstools. Ihre Stärken spielt die Methode aber vor allem bei der Beschreibung von sogenannten Mikroströmungen aus. Mikroströmungen treten zum Beispiel in kleinen Energiewandlern wie Brennstoffzellen für portable Geräte und in den meisten technischen Katalysatoren auf. In solchen Systemen müssen sich Gase oder Flüssigkeiten auf sehr engem Raum oder durch mikroskopisch kleine Poren hindurch bewegen. Die Strömungsvorgänge müssen dann auf der Ebene von einzelnen Teilchen beschrieben werden. Da die Gitter-Boltzmann-Methode gerade auf einer mikroskopischen Theorie von Strömungsvorgängen basiert, ist sie dazu prädestiniert, bei solchen Fragestellungen Anwendung zu finden.
Doch bis zur heutigen Reife musste die Methode einen langen Weg zurücklegen. „Vor 20 Jahren waren die Möglichkeiten, die diese Simulationsmethode anbot, noch recht beschränkt“, erklärt Ioannis Mantzaras, Leiter der Gruppe Grundlagen der Verbrennung am PSI. Mit der reinen Gitter-Boltzmann-Methode, also ohne Zuhilfenahme anderer Tools, liessen sich praktisch nur reine Substanzen bei konstanter Temperatur beschreiben. Das aber liegt selbstverständlich oft fern der Realität.
Immer realistischere Simulationen
In den letzten Jahren haben sich jedoch dank der rasanten Entwicklung der Rechenleistung und Speicherkapazität von Computern sowie durch Verfeinerung der Berechnungsverfahren (Algorithmen) und der physikalischen Modelle zuvor undenkbare Möglichkeiten aufgetan. Wissenschaftler sind heute in der Lage, mit Gitter-Boltzmann sehr komplexe Systeme mit vertretbarem Aufwand realistisch am Computer zu untersuchen.
Davon profitierten auch die PSI-Forscher. Sie haben nun erstmals ein Modell entwickelt, das es möglich macht, mit der Gitter-Boltzmann-Methode die Strömung von Gas- oder Flüssigkeitsmischungen bei veränderlichen Temperaturen zu simulieren. Dazu mussten sie ein schwerwiegendes Manko der bisherigen Gitter-Boltzmann-Modelle für Mischungen beseitigen, nämlich deren Unfähigkeit, ein so wichtiges Naturgesetz wie das der Energieerhaltung auf einfache Weise zu beschreiben. Das gelang ihnen, indem sie die Kollisionen unter den Gasmolekülen geschickt modellierten.
Vorgänge im Hintergrund verstehen und Entwicklungskosten senken
Mit ihrer Arbeit eröffnen die PSI-Wissenschaftler den Zugang zu realitätsnäheren Computersimulationen von vielen komplexen technischen Vorgängen. „Gasmischungen mit veränderlichen Temperaturen kommen in einer Vielzahl technischer Systeme vor: etwa in den meist mikroporösen Strukturen technischer Katalysatoren, in Dieselpartikelfiltern, Verbrennungsmikroreaktoren oder Brennstoffzellen“, sagt Nikolaos Prasianakis, der das Modell mitentwickelte. „Indem man diese Systeme nun am Computer simulieren kann, tragen wir dazu bei, deren Entwicklungskosten künftig zu senken“, sagt Prasianakis. „Man kann am Computer nämlich mehr Szenarien durchspielen als in echten Tests, in denen teure Prototypen zerstört oder beschädigt werden können. Heute wird zum Beispiel kein Auto mehr im Windkanal getestet, bevor sein aerodynamisches Verhalten gründlich am Computer simuliert worden ist.“ Experimente bleiben unentbehrlich, aber mit Hilfe von Simulationen können sie effizienter geplant und durchgeführt werden.
Ausführliche Validierung
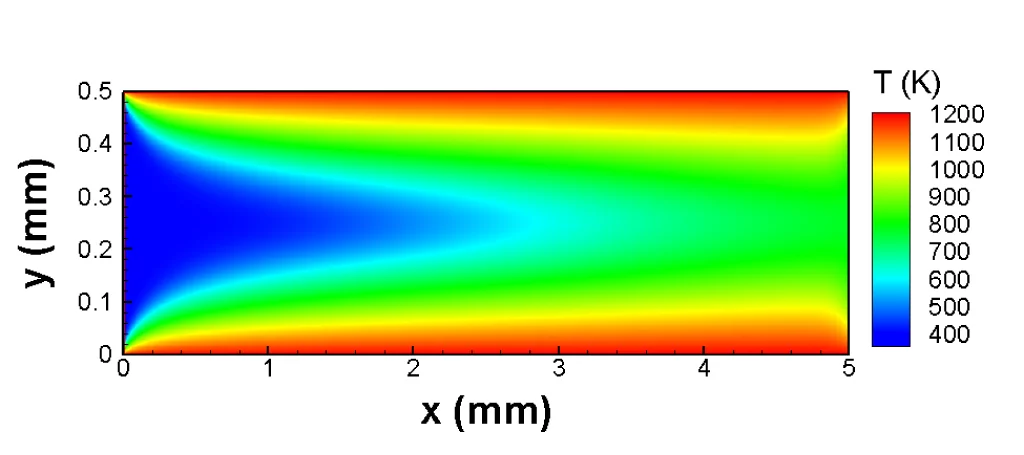
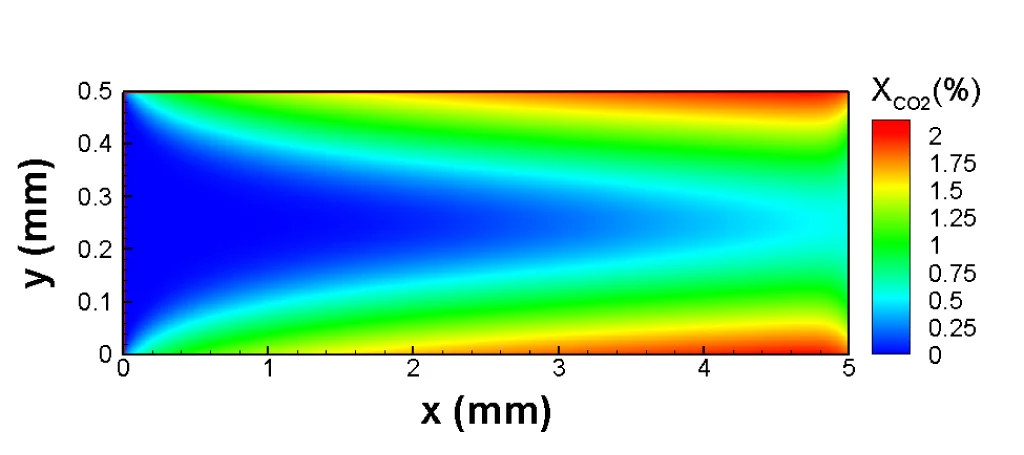
Ebenfalls unumgänglich sind Validierungstests eines jeden Simulationmodells, und sei es in mathematischer Hinsicht noch so fehlerfrei. Deshalb haben die PSI-Forscher ausführlich getestet, ob ihr Modell das Verhalten der simulierten Strömungen richtig wiedergibt. Sie konnten dabei nachweisen, dass ihre Methode zum Beispiel die Änderungen der Schallgeschwidigkeit mit der Temperatur in einem Gas richtig beschreibt. In weiteren Tests zeigten sie, dass ihr Modell Ergebnisse liefert, die mit jenen anderer etablierter Simulationsmethoden übereinstimmen. Das Modell bestand den Vergleich auch in jeden Fällen, für die eine exakte mathematische Lösung bekannt ist. In ihrer nun publizierten Form gilt das Modell zwar nur für zweidimensionale Strömungen einer aus zwei chemischen Substanzen bestehenden Gasmischung. Die Forscher zeigten aber, dass sich das Modell problemlos auf drei Dimensionen und Mischungen aus beliebig vielen Bestandteilen erweitern lässt.
Text: Leonid Leiva
Kontakt / Ansprechpartner
Dr. Ioannis Mantzaras, Leiter der Gruppe Grundlagen der Verbrennung, Paul Scherrer Institut,Telefon: +41 56 310 40 46, E-Mail: ioannis.mantzaras@psi.ch
Originalveröffentlichungen
*Lattice Boltzmann model for thermal binary-mixture gas flows*Jinfen Kang, Nikolaos I. Prasianakis, John Mantzaras
Physical Review E, 87, 053304, 2013.
DOI: 10.1103/PhysRevE.87.053304
Lattice Boltzmann model for the simulation of multicomponent mixtures
S. Arcidiacono, I.V. Karlin, J. Mantzaras, C. E. Frouzakis,
Physical Review E, 76, 046703, 2007.
DOI: 10.1103/PhysRevE.76.046703