Analysis of signal lineshapes is a prominent problem and a theme of importance in physics, chemistry and biomedicine. The problem is exacerbated for multiple peaks in the presence of noise. We demonstrate an algorithm which takes advantage of peak multiplicity (N) to retrieve line shape information. The method is exemplified via analysis of Lorentzian and Gaussian contributions to individual lineshapes for a practical spectroscopic measurement. In addition, our method benefits from a linear increase in sensitivity with the number N in stark contrast to other methods facing increased computational overhead. Moreover, we show the method to be robust in terms of noise reduction and exhibit an order of magnitude improvement in run-time performance. Our results are applicable to a wide range of topics, ranging from neutron-scattering to spectroscopy of rare-earth doped solids.
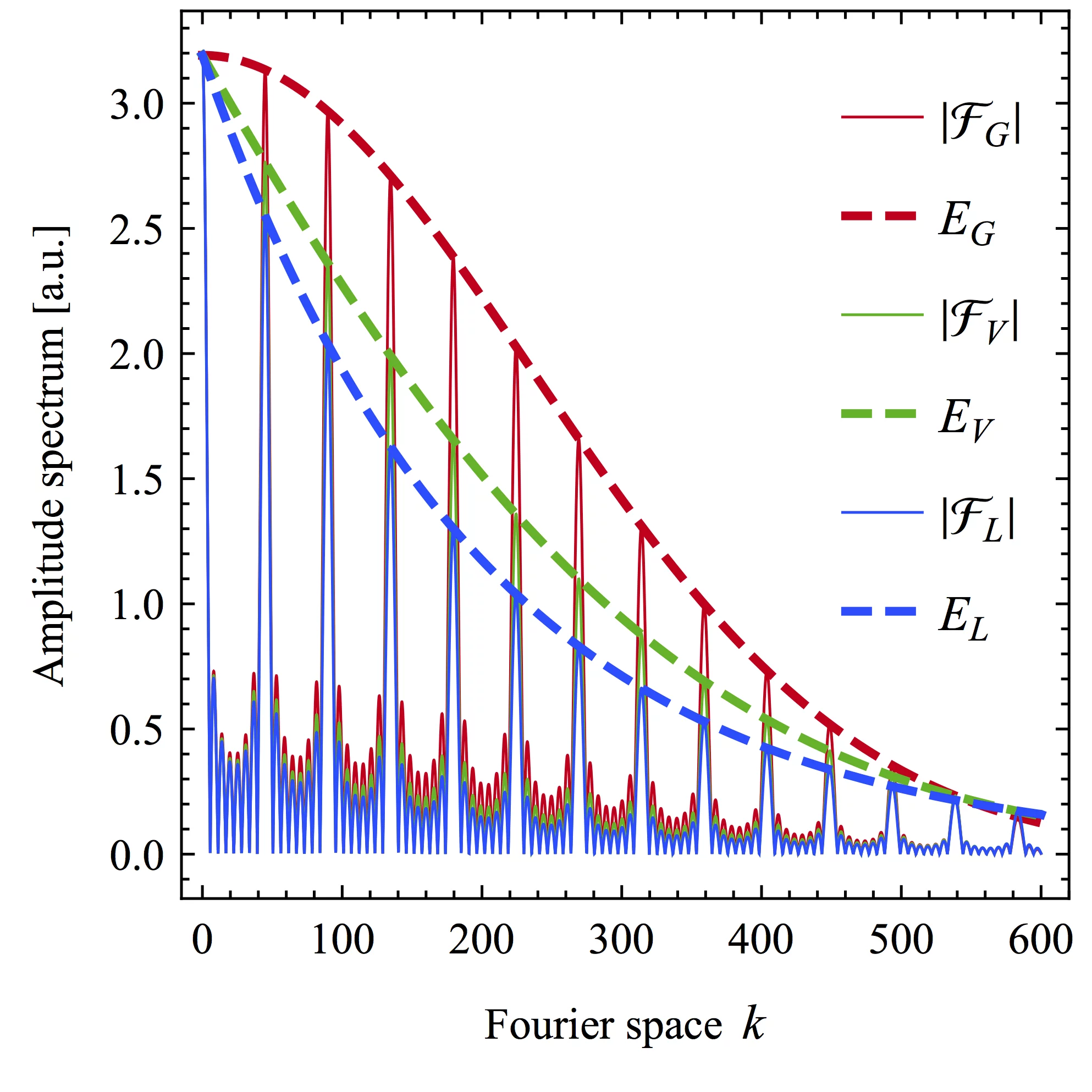
The individual line shape of a multiplet line translates to a peculiar envelope in Fourier space. The Fourier transform (solid) and its envelope (dashed) are shown for three cases: Lorentzian (blue), Gaussian (red) and Voigt (green).
Original Publication
Taking advantage of multiplet structure for lineshape analysis in Fourier space
Adrian Beckert, Hans Sigg, and Gabriel Aeppli
Optics Express Vol. 28, Issue 17, pp. 24937-24950,(2020)
DOI:https://doi.org/10.1364/OE.395877
Contacts
Adrian Beckert
Laboratory of Micro- and Nanotechnology
Paul Scherrer Institut, Forschungstrasse 111, 5232 Villigen PSI, Switzerland
Telephone: +41 56 310 2580, email: adrian.beckert@psi.ch [English]
Dr. Hans Sigg
Laboratory of Micro- and Nanotechnology
Paul Scherrer Institut, Forschungstrasse 111, 5232 Villigen PSI, Switzerland
Telephone: +41 56 310 4048, email: hans.sigg@psi.ch [English, German]