Even though experimental results or numerical simulations typically have a high dimensionality (degrees of freedom), they can often be well-characterized by (low-dimensional) dominating coherent structures. In this context it is worth mentioning, that in contrast to the increasing availability of highly resolved data obtained from experiments and numerical simulations, there is a correspondingly significant need to describe high-dimensional fluid systems in a more elementary fashion. This is because low-dimensional data could highlight certain flow features that are otherwise masked (and are therefore not accessible) because of the complexity of the fully turbulent flow. These reduced order models (ROMs) effectively filter out the small-scale turbulent structures which do not contribute much to the convergence towards a valid representation of the essential flow physics according to [2] . Proper Orthogonal Decomposition (POD) is a mathematical framework to extract and characterize these large-scale structures, as initially outlined and suggested by Lumley [3]. A mathematical framework is a set of adequate equations comparable to a tool-box a plumber carries with him when he is called.
The POD algorithm separates the spatio-temporal ensemble of velocities U into space-dependent orthonormal POD modes (spatial modes, also referred to as the basis functions) and time-dependent orthogonal modes (referred to as temporal modes), respectively. For the algorithm on how to calculate the POD decomposition for a given ensemble of velocity fields or other data see [4]. It is worth mentioning at this point, that the spatial and temporal modes are a priori unknown and have to be derived from the data itself. In that, the POD method is data driven.
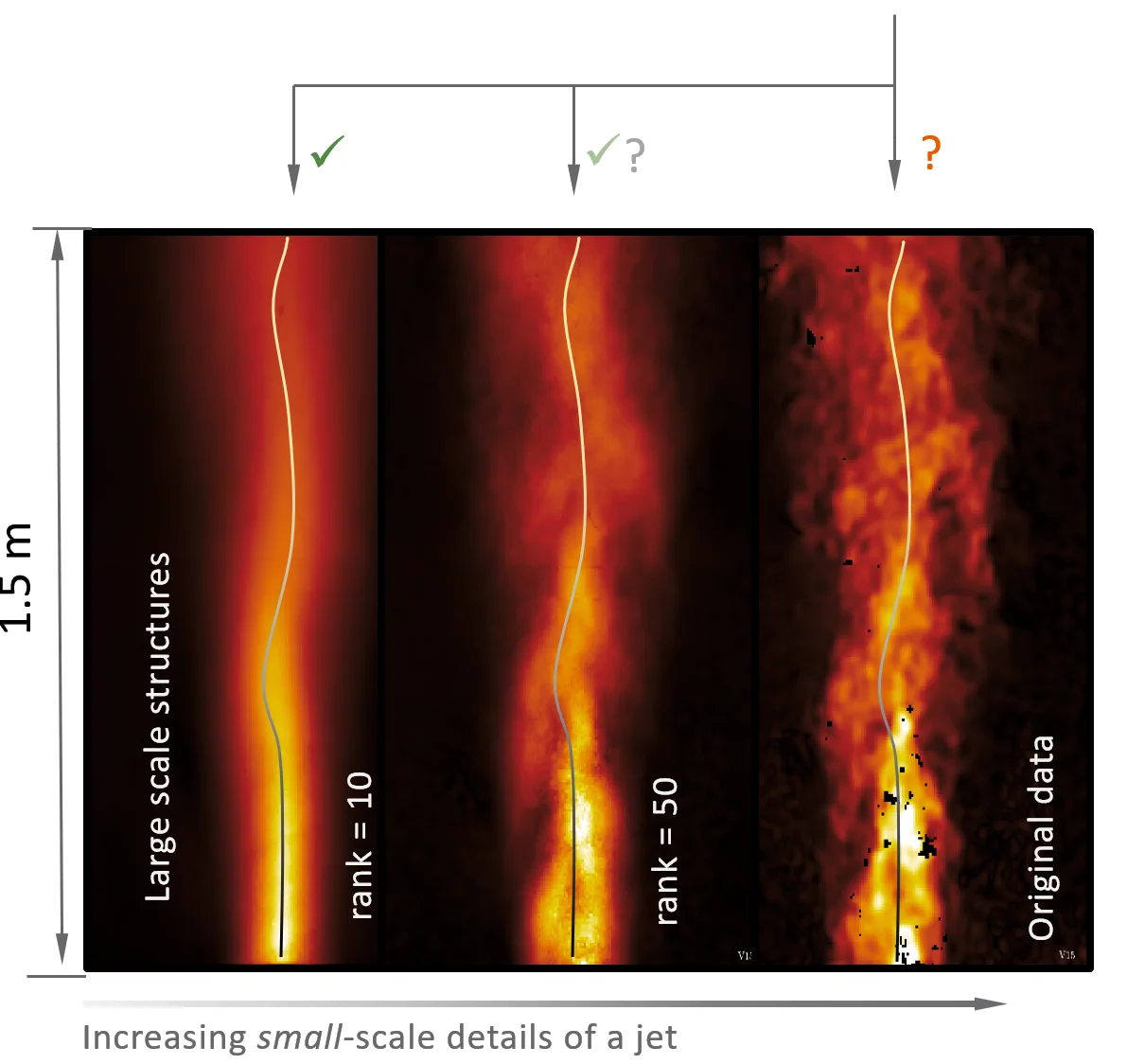
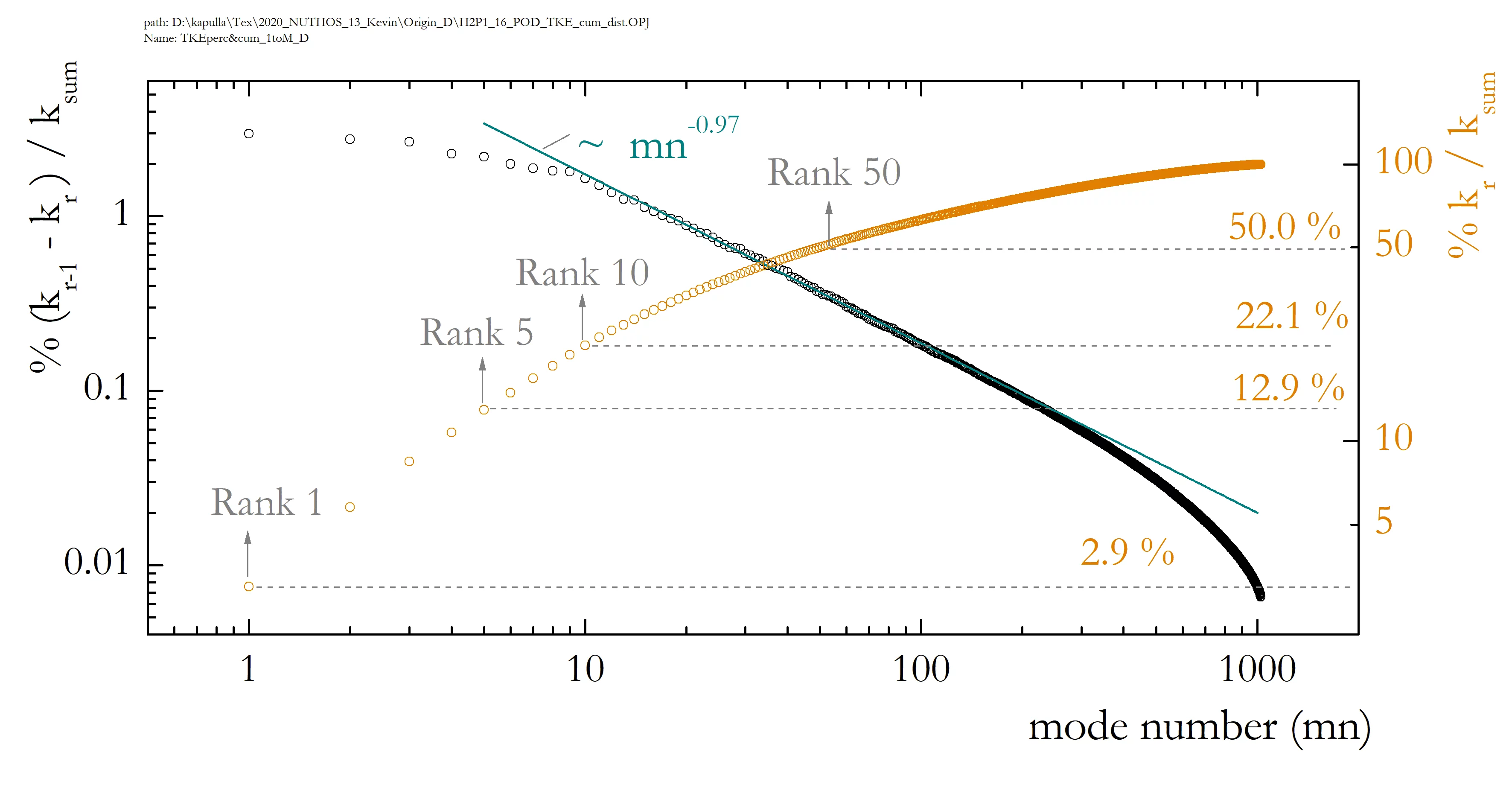
The predominant method in the literature to select the relevant basis functions for the final approximation is based on the energy of the flow the spatial modes represent. An example of the energy distribution among the spatial modes for the jet under consideration is presented below.
In total, the energies distribute across nearly three orders of magnitude from mode 1 to mode 1024; the latter depicting the maximum number of snapshots recorded. For the mode energies, we observe a distinct slope change around mode 10, i.e. we find energies within the same order of magnitude for mn<10 whereas the energies past mn>15 decay more rapidly. The former region is usually attributed to the importance these modes have for the reconstruction of the flow field. In contrast to this, it was possible to show, that spatial modes which are usually not caught by a pure energy-based criterion also play an important role in the reconstruction of the flow field. A refinement of this energy criterion for the relevant modes to be considered for the truncation can be found in [5].
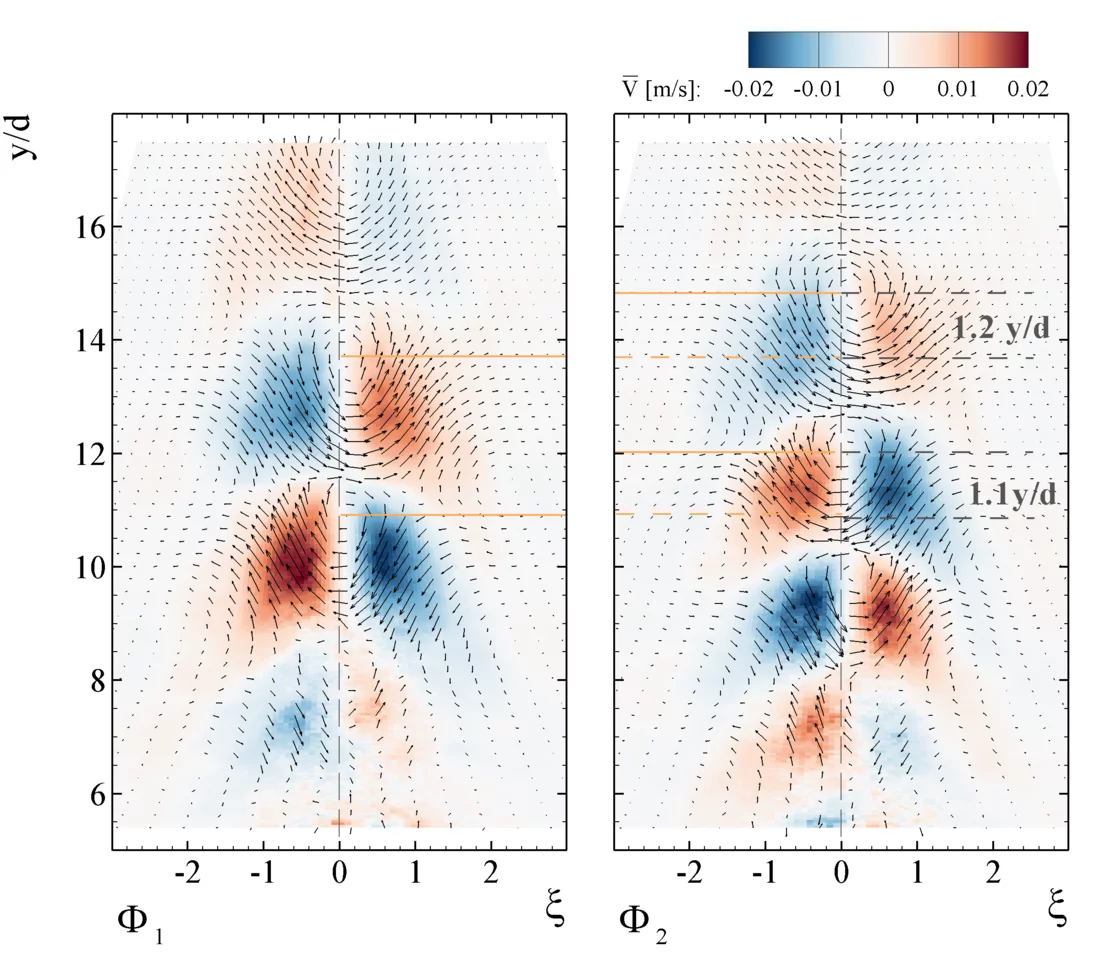
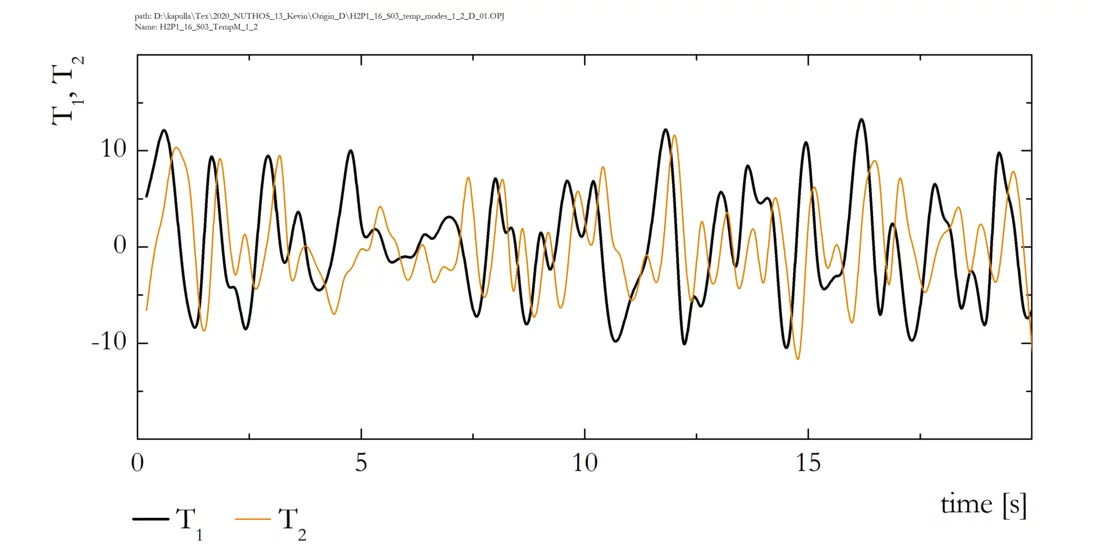
Examples of the resulting spatial and temporal modes are presented below. The spatial structures of the first two spatial modes and are almost identical showing the presence of 3 successive large-scale vortical structures. This opens the door for a refined analysis of these structures and their importance towards the route to and their importance for self-similarity of the entire flow field. A classical subject of fluid dynamics.
The suggested POD method – exemplified with experimental 2D velocity data – can be extended to 3D data[6] .
Contact
Dr. Ralf Kapulla
Experimental Thermal Hydraulics Group (TEG)
Laboratory for Reactor Physics and Thermal-Hydraulics (LRT)
Nuclear Energy and Safety Research Division (NES)
Paul Scherrer Institut
Original Publications
[1] G. Lipari, P. K. Stansby
Review of experimental data on in-compressible turbulent round jets
Flow, Turbulence and Combustion 87 (2011) 79– 114.
[2] N. Ali, N. Hamilton, D. DeLucia, R. Bayoán Cal
Assessing spacing impact on coherent features in a wind turbine array boundary layer
Wind Energy Science 3 (2018) 43–56.
[3] J. L. Lumley
The structure of inhomogeneous turbulent flow
Atmospheric Turbulence and Radio Propagation, 1967
[4] L. Sirovich
Turbulence and the dynamics of coherent structures. Part I
Quaterly of Applied Mathematics (1987) 561–571.
[5] R. Kapulla, K. H. Manohar, S. Paranjape and D. Paladino
Self-similarity for statistical properties in low-order representations of a large-scale turbulent round jet based on the proper orthogonal decomposition
Experimental Thermal and Fluid Science, Volume 123, 2021, 110320