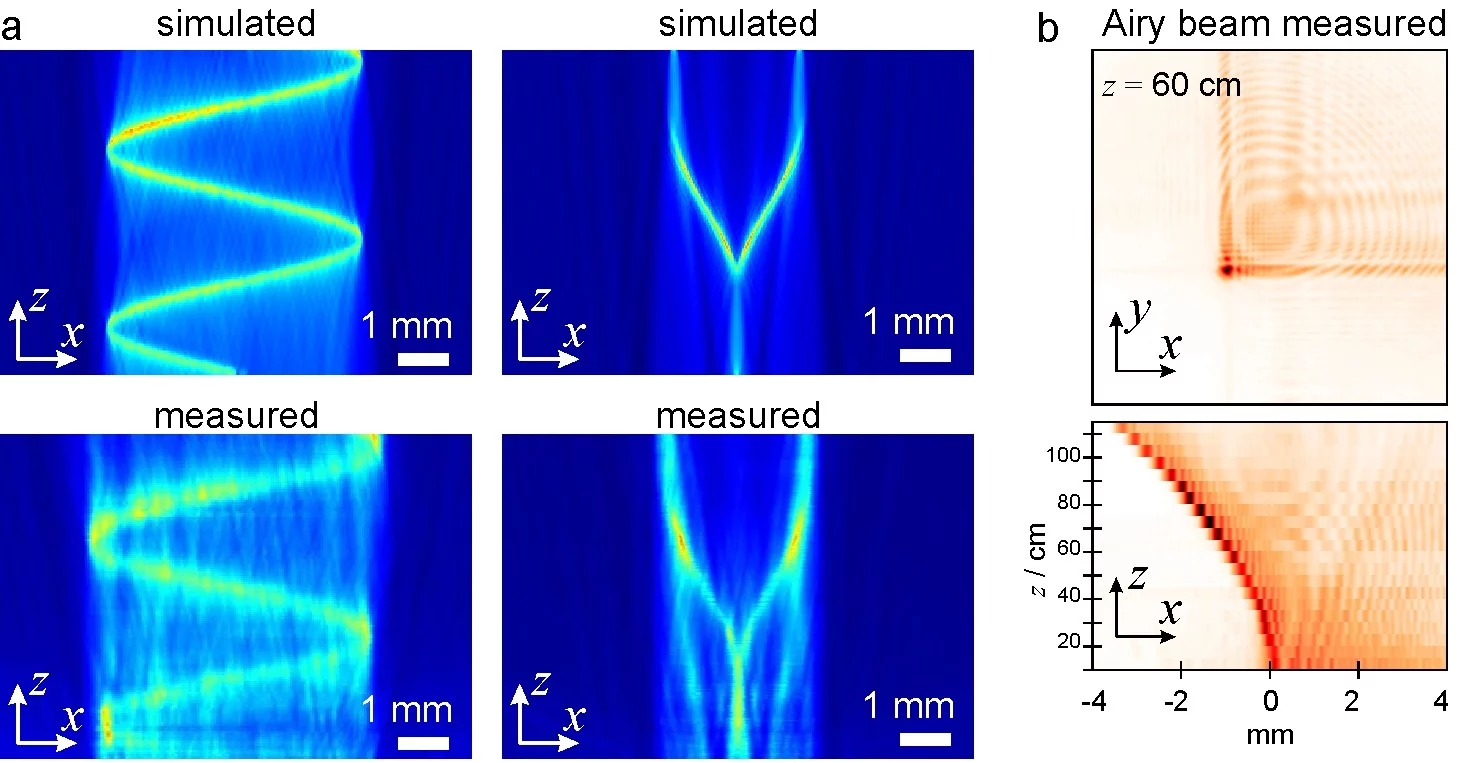
Bending light on demand or 3D arbitrary-shaped light beams
A classical light beam propagates along a straight line and does not bend unless in a medium of variable refractive index. By modifying the wavefront in a certain manner, the light intensity can be turned into a certain shape. Examples are optical lenses or Fresnel Zone Plates for focusing an incident wave to a point at the focal plane. Another example are Airy beams [1] created by modifying the phase distribution of the wavefront into an Airy function resulting in a bending of the light intensity while propagating (figure). A light beam can be turned into an arbitrary three-dimensionally (3D) curved light beam (figure). To create an arbitrary 3D beam of intensity, the beam trajectory is represented as a sequence of closely packed individual point-like absorbers thus giving a 3D object, and a hologram of this 3D object is simulated. When such a hologram is illuminated, the object in the form of 3D a curve made of dark points is reconstructed. When the contrast of the hologram is inverted, the object in the form of the 3D curve made of bright points is reconstructed, thus creating a 3D curved light beam [2].
1. T. Latychevskaia, D. Schachtler, H.-W. Fink, Creating Airy beams employing a transmissive spatial light modulator, Appl. Opt. 2016, 55, (22), 6095–6101.
2. T. Latychevskaia, H.-W. Fink, Inverted Gabor holography principle for tailoring arbitrary shaped three-dimensional beams, Sci. Rep. 2016, 6, 26312.