Currently, there is a clear understanding of the fact that in many cases the use of representation analysis RA (decomposition of the magnetic representation into irreducible representations irreps) together with Shubnikov group symmetry or with magnetic superspace 3D+n groups allows one to find a hidden symmetry, which is not evident from the RA alone [1]. Identifying of the new symmetry that appears below a phase transition (even without the specific details of the magnetic structure) often allows one to identify the key physical properties of the new phase. One can distinguish several cases when the use of symmetry is essential and profitable. (i) The magnetic propagation vector is not a single one but has several arms (multi-k). The recent example is topologically non-trivial skyrmionic structure in CeAlGe [2]. Using supersymmetry we have found 3D+2 dimensional structure with the superspace group I4_1md1’(a00)000s(0a0)0s0s, which hosts particle like obgects, merons (Fig. 1), which are responsible for the topological Hall effect. In one-k paradigm the structure is a trivial cycloid. (ii) In case of multidimentional irreps we are interested in finding the maximal symmetry solution. RA approach in this case leads to the lowest possible magnetic symmetry. The combined approach not only gives the maximal symmetry solutions, but it also automatically includes some secondary spin degrees of freedom (if they are allowed by magnetic symmetry), which are not accessible from RA-alone [3,4].
Figure 2 shows rather complex magnetic structure in Tb14Ag51 (P6/m) with Shubnikov group P-6' [4], being maximal symmetry subgroup of parent space group P6/m. The model allows the presence of secondary order parameter with k0=0, in addition to the main k-vector star k=±[1/3,1/3,0], which is effectively 3rd harmonics of k. In RA the magnetic symmetry would be rather low - monoclinic Pm'. (iii) We are interested in the exact crystal symmetry space group below the magnetic phase transition. For instance, a specific magnetic structure solution can dictate the charge ordering pattern [3], or the presence and direction of electric polarisation in the multiferroics.
There are many other interesting examples. We promote to use the combined approach for the analysis of the new magnetic structures and also to revisit some already published structures analysed only with RA. The new structures can be added in the database [5] maintained by Bilbao crystallographic server. The database is a collection of magnetic structures with full symmetry description and contains already more that 1570 entries.
References
- IUCr Commission on Magnetic Structures http://magcryst.org
- Pascal Puphal, Vladimir Pomjakushin, Naoya Kanazawa, Victor Ukleev, Dariusz J. Gawryluk, Junzhang Ma, Muntaser Naamneh, Nicholas C. Plumb, Lukas Keller, Robert Cubitt, Ekaterina Pomjakushina, and Jonathan S. White, "Topological Magnetic Phase in the Candidate Weyl Semimetal CeAlGe", PHYSICAL REVIEW LETTERS 124, 017202 (2020)
- F. Li, V Pomjakushin, T. Mazet, R. Sibille, B. Malaman, R. Yadav, L. Keller, M. Medarde, K. Conder, and E. Pomjakushina, "Revisiting the magnetic structure and charge ordering in La1/3Sr2/3FeO3 by neutron powder diffraction and Mossbauer spectroscopy", PHYSICAL REVIEW B 97, 174417 (2018); F. Li, V Pomjakushin, et al "Study of La1/3Sr2/3FeO3 by neutron single-crystal diffraction and neutron spherical polarimetry", to be published
- V Pomjakushin, et al "Revisiting the antiferromagnetic structure of Tb14Ag51. The importance of distinguishing alternative symmetries for a multidimensional order parameter", to be published (2021); Fischer, P., Pomjakushin, V., Keller, L., Daoud-Aladine, A., Sikora, W., Dommann, A. & Hulliger, F., PHYSICAL REVIEW B 72, 134413 (2005)
- Bilbao database of published commensurate and incommensurate magnetic structures - http://webbdcrista1.ehu.es/magndata/
Collaboration
- E. Pomjakushina, LMX/PSI
- J. White, L.Keller, LNS/PSI
- J.M. Perez-Mato, Universidad del Pa ́ıs Vasco, UPV/EHU, Bilbao, Spain
- A. Doenni, M. Hase, National Institute for Materials Science (NIMS), Japan
Alumni
- Fei Li, PhD, ETHZ 2019
- Ch. Mielke, Master Thesis, Univ. of Montpellier/PSI, 2020

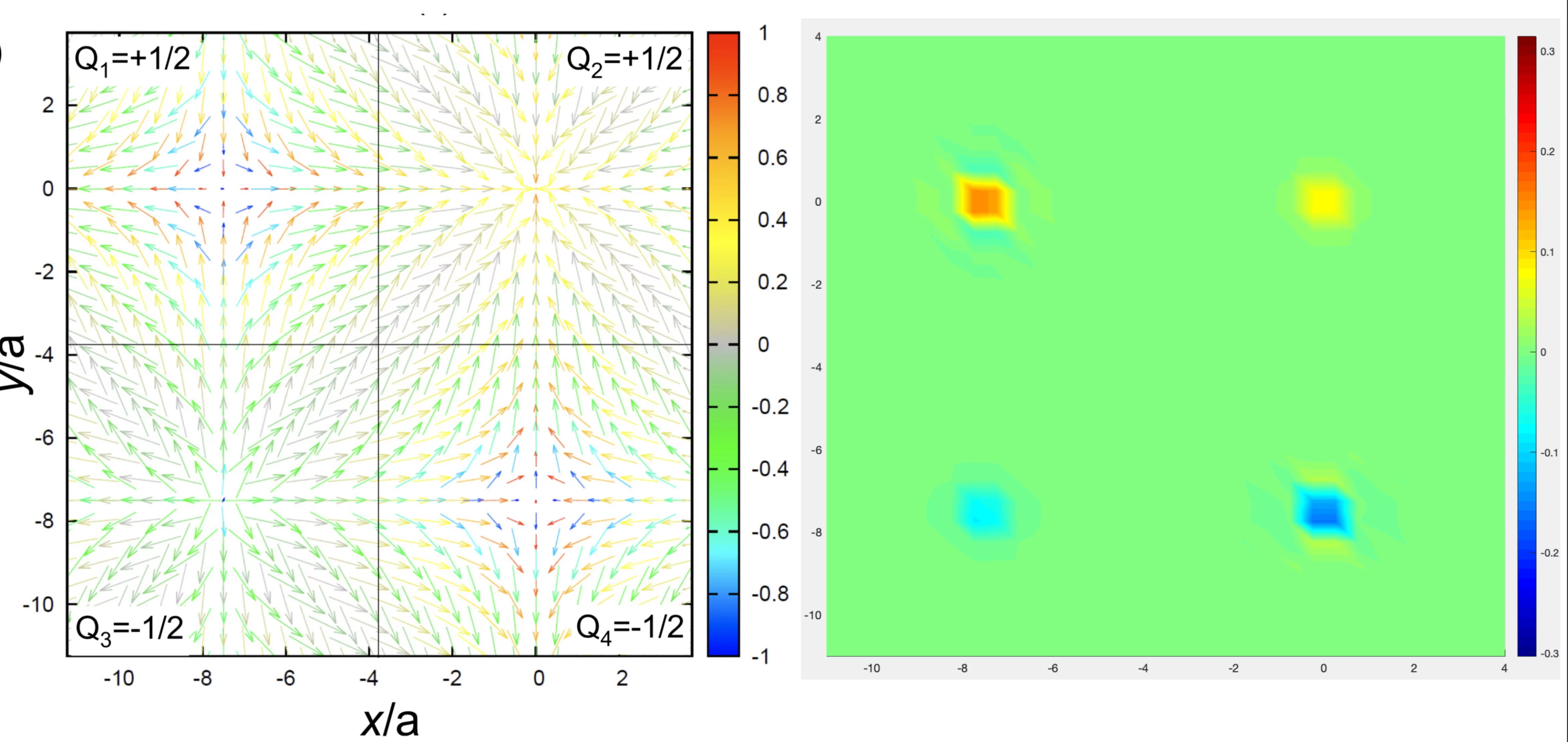
![Fig. 2 View of the magnetic structure formed by Tb-moments in projection on xy-plane corresponding to the maximal symmetry model P-6' of hexoganal Tb14Ag51 (P6/m). The model allows the presence of secondary order parameter with k0=0, in addition to the main k-vector k=[1/3,1/3,0], which is effectively 3rd harmonics of k.](/sites/default/files/styles/primer_full_image_xxl/public/2021-08/Fig2_rect.jpg.webp?itok=goODKKeg)