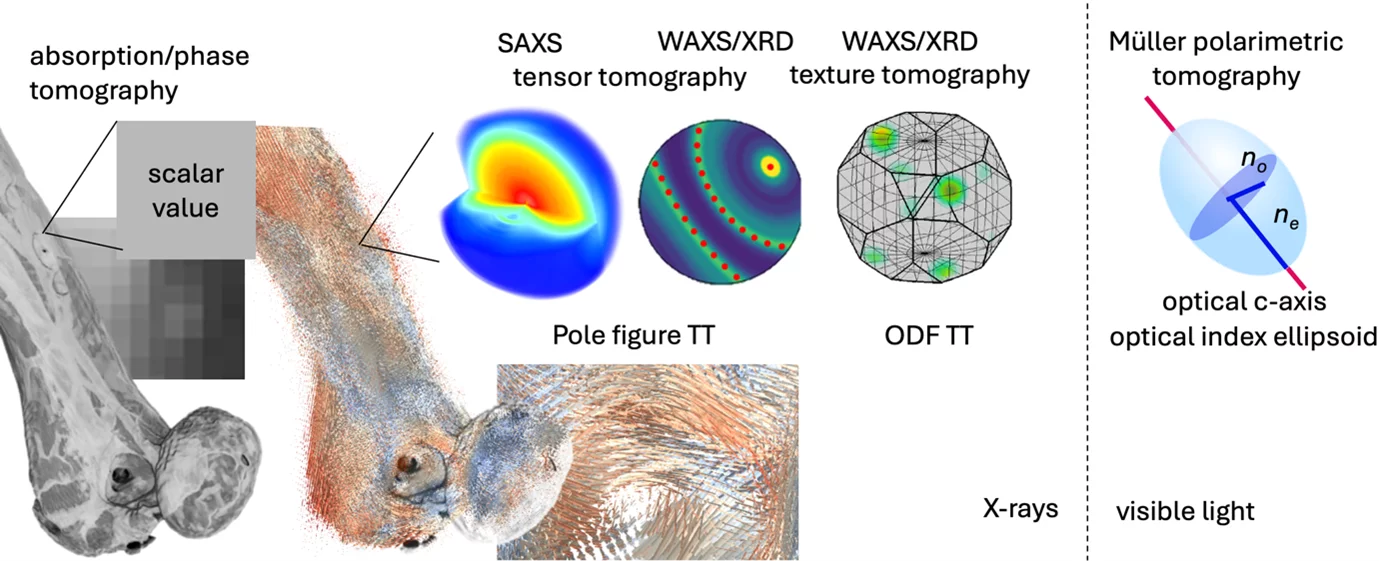
Hierarchical materials show ordering on many length scales for an optimized functionality as illustrated on the example of bone. With tensor tomography the orientation of nanostructure in each subvolume or voxel is mapped over an extended macroscopic sample in three dimensions. Compared to standard computed tomography, where each sub volume, called voxel, contains a grey scale value, tensor tomography aims to reconstruct a tensor in each voxel. For SAXS tensor tomography this tensor represents a model for the full 3D reciprocal space map which contains information on shape, size and arrangement of nanostructure.
Compared to standard tomography, we need to measure projections around two perpendicular tomographic axis to acquire enough information to solve the 6D-tomography.
ERC Starting Grant MUMOTT – Multi Modal Tensor Tomography
At the core of MUMOTT lays the development of the methodological framework implemented in an open-source software package allowing for the reconstruction of tensors in each sub-volume or voxel of the three-dimensional tomogram. The main modes in focus of MUMOTT are small-angle X-ray scattering (SAXS), wide-angle X-ray scattering (WAXS), and birefringence of visible light.
Apart from the methodology framework we are implement the different modes to prove their capability to solve critical problems in materials and bio-science; to investigate the structure of light-weight composites based on cellulose nanofibrils, reveal how the arrangement of nanoparticles in a plasmonic composite is connected to its sensing capabilities, as well as shed light on the disruptive collagen network in breast cancer.
Part of the work within MUMOTT is conducted in the research group located at Chalmers University of Technology, Gothenburg, Sweden.
Tensor Tomography Method development
For SAXS tensor tomography, we developed robust algorithms to resolve complex textures and allow for fast reconstruction times.
Nielsen L.C., Erhart P., Guizar-Sicairos, M. & Liebi, M.*
"Small-angle scattering tensor tomography algorithm for robust reconstruction of complex textures"
Acta Cryst A. 2023, 79, 515-526 DOI: 10.1107/S205327332300863X.
This allows to resolve multi-directions within a single voxel, however, the more flexibility is allowed in the optimization algorithms, the more one has to be careful from artefacts from the missing-wedge, i.e. the data we are lacking in the two tomographic axis needed for the reconstruction by blocking of the sample mount.
Nielsen L.C., Tänzer, T., Rodriguez-Fernandez I. Erhart P., & Liebi M.*
"Investigating the missing wedge problem in small-angle x-ray scattering tensor tomography across real and reciprocal space."
J. Synchrotron Rad., 2024, 31, 1327-1339 DOI: 10.1107/S1600577524006702
Enforcing known symmetries, such as common point and axial- symmetry, also referred to as fiber symmetry, are very helpful to reduce the artefacts from the missing wedge, which we have shown in WAXS tensor tomography on metal wire, which exhibit strong texture.
Carlsen, M.*, Appel, C., Hearn, W., Olsson, M., & Liebi, M.*
"X-ray tensor tomography for small-grained polycrystals with strong texture."
J. Appl. Crystallogr., 2024, 57(4) 986-1000. DOI: 10.1107/S1600576724004588
If the crystal symmetry is directly connected to the reconstruction of several Bragg peak at once, we can release sample requirements even more. We have shown in an implementation of texture tomography making use of sparsity that reconstruction with a single tomography axis is feasible.
Carlsen, M.*, Malamud, F., Modregger, P., Wildeis, A., Hartmann, M., Brandt, R., Menzel A. and Liebi, M.
"Texture tomography with high angular resolution utilizing sparsity."
J. Appl. Crystallogr., 2025 58, 484–494. DOI: 10.1107/S1600576725001426
Measurement times for tensor tomography are very long, due to the combination of raster scanning to acquire a single 2D projection, and repeating many projections, in most cases around two tomographic axis. Optimized implementation at a macro-crystallography beamline at PSI (PX-I) enabled a large reduction in measurement times.
Appel, C., Schmeltz, M., Rodriguez-Fernandez, I., Anschuetz, L., Nielsen, L. C., Panepucci, E., Marijolovic, T., Wakonig, K., Ivanovic, A., Bonnin, A., Leonarski, F., Wojdyla, J., Tomizaki, T., Guizar-Sicairos, M., Smith, K., Beale, J. H., Glettig, W., McAuley, K., Bunk, O., Wang, M.*, Liebi, M*.
"Fast Small-Angle X-ray Scattering Tensor Tomography: An Outlook into Future Applications in Life Sciences."
https://arxiv.org/abs/2406.13238
Tensor tomography based on the birefringence of optical light was developed which allows to reconstruct the optical index ellipsoid in each voxel using a rather simple and low-cost setup. This allows to retrieve 3D ultrastructure orientations in 3D using visible light, a method we refer to as Tomographic Müller-Polarimetric Microscopy .
Chen, Y.*, Baroni, A.*, Tänzer, T., Nielsen, L. & Liebi, M.*
Reconstructing Three-Dimensional Optical Anisotropy with Tomographic Müller-Polarimetric Microscopy.
Advanced Science 2502075 (2025). DOI: 10.1002/advs.202502075
All reconstruction codes are published open-source and various data are published on Zenodo.
As of June 2023, the first version of the all-Python package for the analysis of tensor tomography measurements, MUMOTT 1.0, has been released, and is constantly updated. For more information, go to mumott.org and Gitlab. The current implementation supports SAXS and WAXS tensor tomography. Additional branches are available for texture tomography Gitlab using sparsity and Tomographic Müller-Polarimetric Microscopy.
The package is described in the accompanying software paper:
Nielsen L.C., Carlsen M., Wang S., Baroni, A. Tänzer, T., Liebi M.*, Erhart, P.*
"Mumott -- a Python package for the analysis of multi-modal tensor tomography data"

