Hydrogen spectroscopy
Present knowledge of the (root-mean-square) proton charge radius which does not depend on hydrogen spectroscopy comes from electron scattering experiments. A recent reanalysis of all electron-proton scattering data [1], accounting for Coulomb distortion and using a parametrization that makes it possible to include data at higher q2, finds a radius of 0.895(18) fm, i.e. the uncertainty is as large as 2%.
The ultra-precise measurements in hydrogen of the 1S-2S [2] and 2S-nS/nD [3] transitions yield precise values for the Rydberg constant and the Lamb shift of the 1S ground state. Comparison of the Lamb shift measurements with theory (bound-state QED) is limited by the uncertainty of the proton charge radius. In fact its main uncertainties are: from experiment (2 ppm), QED calculations (1 ppm), and proton size (6 ppm).
An effort is going on to reduce both the experimental and theoretical uncertainties below the ppm level. Currently, attention is directed towards two-loop corrections, as they give the largest uncertainties in the theoretical predictions. These corrections have very peculiar features, not encountered anywhere else. The power series in Zα has slow convergence. The presence of many logarithmic terms ln(Zα), and the fact the higher-order coefficients in this series could be orders of magnitude larger than the leading ones, makes it difficult to estimate the non-calculated terms in the power series expansion. For that reason attempts to calculate numerically the two-loop correction in all orders are being made [4]. However these results are available only for hydrogen-like ions with Z≥10. A current theoretical prediction for the 1S Lamb shift in hydrogen [5],
L1Sth=8172811 (4)(51) kHz,
can be compared with the experimental result:
L1Sexp=8172837 (22) kHz.
The first uncertainty in the theoretical value is due to uncalculated higher order terms, whereas the second one comes from the proton radius. The close agreement indicates that QED is correct whithin the present limits of theory and experiment. The large uncertainty due to the proton radius can be reduced by a factor 20 by measuring the 2S Lamb shift in muonic hydrogen (μp).
High precision measurements of both the μp Lamb shift and the Rydberg constant are expected to provide a test of bound-state QED approaching the 10-7 level. In addition precise knowledge of the proton radius is also helpful in the developement of proton models (form factors, magnetic distribution, Zemach radius, proton polarizability, and low energy QCD calculations).
[1] I. Sick, Phys. Lett. B 62, 576 (2003).
[2] M. Niering et al., Phys. Rev. Lett. 84, 5496 (2000).
[3] B. de Beauvoir et al., Eur. Phys. J. D 12, 61 (2000).
[4] V.A. Yerokhin et al., Phys. Rev. A 71, 040101 (2005).
[5] K. Pachucki and U.D. Jentschura, Phys. Rev. Lett. 91, 113005 (2003).
Muonic hydrogen Lamb shift
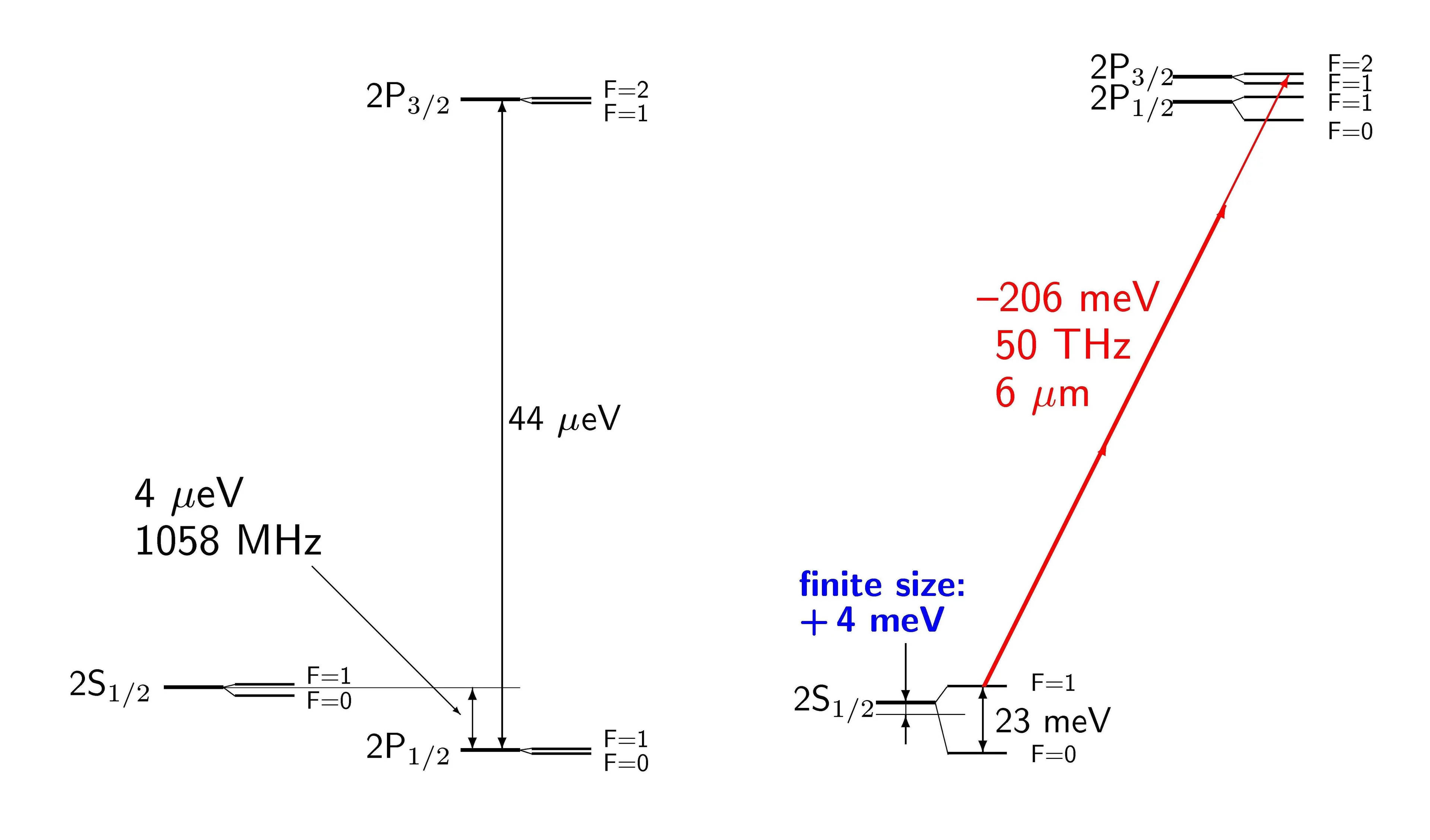
The μp Lamb shift, ΔE(2P-2S) ≈ 0.2 eV, is dominated by vacuum polarization which shifts the 2S binding energy towards more negative values (see figure). The μp fine- and hyperfine splittings are an order of magnitude smaller than the Lamb shift. The relative contribution of the proton size to ΔE(2P-2S) is as much as 1.8%, two orders of magnitude more than for normal hydrogen atoms.
The muonic Lamb shift ΔE(2P-2S) was recalculated recently by several authors [1-3] considering all QED contributions at the ppm level, including three-loop vacuum polarization, hadronic vacuum polarization, light-by-light scattering, and recoil corrections to the order α6. The uncertainty in the calculated proton polarization shift will ultimately limit the calculated ΔE(2P-2S)-value to the 0.3 ppm precision level (disregarding terms which depend on the proton radius).
The theoretical prediction for the muonic hydrogen Lamb shift is
ΔE(2PF=2 - 2SF=1)=205.952 (3)(4)(137) meV
where the first error is the uncertainty of the calculated QED-terms, the second one the uncertainty from the proton polarization, and the third one the uncertainty given by the poor knowledge of the proton radius.
A measurement of the muonic Lamb shift with 30 ppm precision will hence determine the proton radius with 0.1% precision.
[1] K. Pachucki, Phys. Rev. A 60, 3593 (1999).
[2] M.J. Eides et al., Phys. Rep. 63, 342 (2001).
[3] E. Borie, Phys. Rev. A 71, 032508 (2005).