Technical systems like nuclear reactors are complex in nature and therefore require the coupling of several mathematical models and sub-models in order to describe and analyse them. These mathematical models are typically implemented in computational codes used for safety analysis and accident scenario evaluations of nuclear reactors, thereby ensuring the safe operation of these systems. The models used in the analyses of nuclear reactors can be broadly classified into the following categories: (1) Basic nuclear physics models used in nuclear data evaluations, (2) models implemented in nuclear data processing codes, (3) neutron transport models including reactor kinetics, (4) models implemented in thermal-hydraulics and computational fluid dynamic codes, (5) reactor fuel mechanics models, and (6) reactor dosimetry models, among others [1].
These models interact with each other since the output of some models called lower-level models are normally used as input to other models (higher-level models). Furthermore, different experimental data sets are utilized for the calibration and validation of these models at each level. For example, differential experimental data are used for validating and calibrating nuclear reaction models implemented in codes such as TALYS, while integral benchmark data are used for the validation of neutron transport models implemented in codes such as the MCNP® (Monte Carlo N-Particle code) Software.
This makes it particularly difficult and computationally expensive to integrate or combine the various activities over the entire calculation chain into a single process. With the increase in computational power and improvements in nuclear reaction theory, a novel approach called ’Total Monte Carlo’ (TMC) was developed with a goal of propagating uncertainties from basic physics parameters to applications and for the production of the TENDL library. This work presents an approach for combining differential and integral experimental data for data adjustment and uncertainty propagation within a TENDL library framework.
Methodology: Bayesian incorporation of prior knowledge
A statistically rigorous way to combine experimental information with theoretical models is using Bayes theorem of conditional probability. Within a Bayesian framework, the posterior distribution defined as the updated probability distribution of a set of parameters given experimental data, is considered proportional to the product of the likelihood function and the prior distribution. The prior distribution expresses our initial belief before the introduction of experimental data while the likelihood function provides a measure of the goodness of fit of our models to experimental data.
Now, given that we have a prior distribution of model parameters and a likelihood function - the probability of the experimental data given model parameters; we can compute the posterior probability distribution with an updated (weighted) mean and a corresponding weighted variance. In this work, two sets of experiments were considered: (1) differential experiments and (2) integral benchmark experiments.
The differential experimental data are microscopic quantities that describes the properties of a nucleus and its interaction with incident particles such as neutrons and protons while integral benchmark data are quantities that describe the global behavior of a given system. These quantities, in the case of nuclear reactors include, the effective multiplication factor, the effective delayed neutron fraction and the neutron flux, among others.
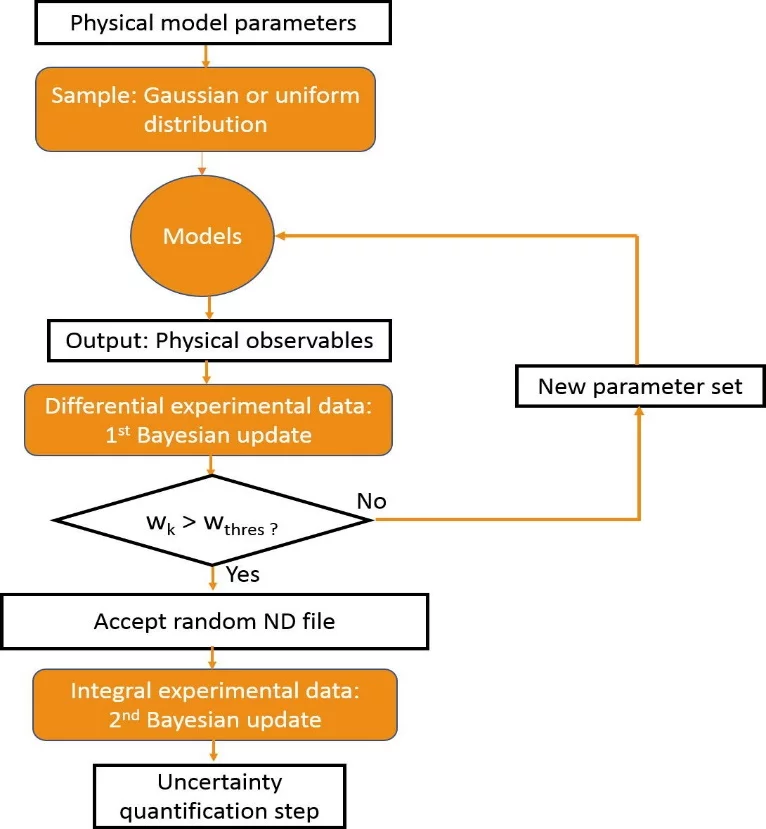
In Fig. 1, a flowchart showing the Bayesian updating scheme used in this work is presented. The first step is to identify the model parameters that play significant roles in characterizing the cross sections of interest. Next, we choose the distributions from which our model parameters would be drawn. Usually, the Gaussian or uniform distributions are used. We then run the TALYS code, which contains our nuclear reaction models, multiple times - each time with a different set of model parameters drawn from our chosen distribution - to obtain outputs such as cross sections, angular distributions, etc.
The final step involves carrying out a probabilistic data assimilation within a Bayesian framework. Two separate Bayesian updates are performed: (1) using only differential experimental data, and (2) using integral experimental data. The main objective of this work is to combine the individual likelihood functions from each update into a global (or combined) likelihood function for each nuclear data (ND) file. The combined likelihood function is used in our optimization procedure for the selection of the ‘best’ file – the random nuclear data file which maximizes the combined likelihood function.
Application: n+208Pb
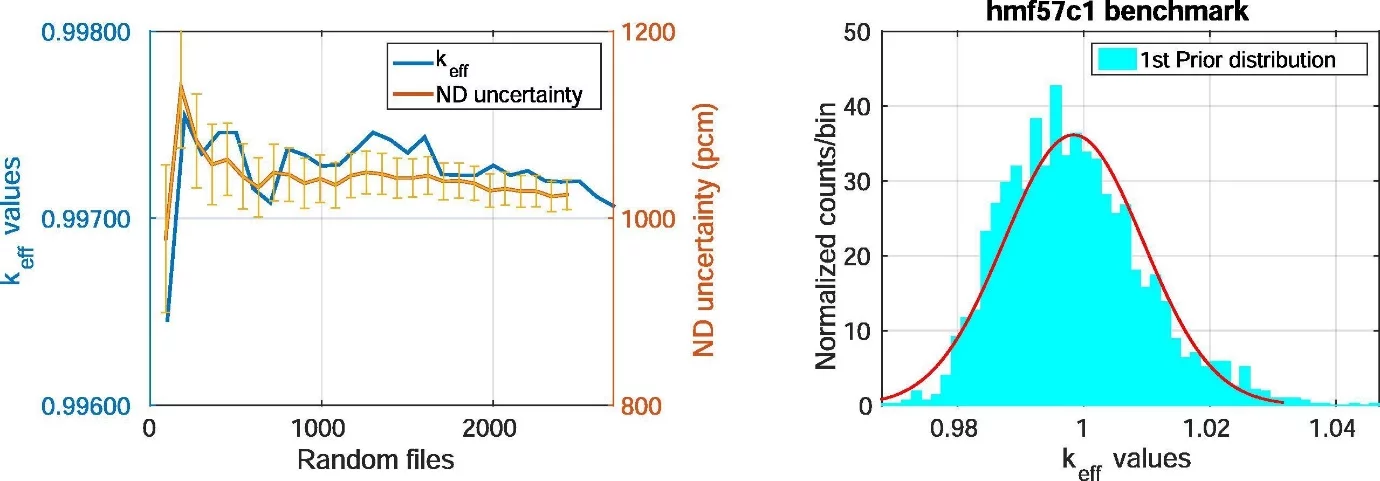
As a proof of principle, the method presented has been applied for the adjustment of neutron-induced reactions on 208Pb in the fast incident energy region. Lead is used for radiation shielding against high energy radiations such as gamma rays and x-rays. In addition, molten lead has been proposed as a coolant for Lead-Cooled Fast reactors within the generation IV reactor programme. It should be noted here that, 208Pb makes up about 52.4% of natural lead. A total of 2500 random nuclear data files (in the ENDF format) were produced using the TALYS code system. These random nuclear data files were first processed into x-y tables for comparison with selected differential experimental data. The random ENDF files were then processed into usable formats and then fed into the MCNP neutron transport code to produce a distribution of keff (the effective multiplication factor) for the benchmark of interest. In order to determine if the random nuclear data files for the (prior) keff distribution had converged, the mean with its corresponding 208Pb nuclear data uncertainty, is plotted against the number of random files for a number of iterations and presented in Fig. 2 (left). The keff distribution was obtained by varying 208Pb nuclear data in the HMF57 case 1 (HEU-MET-FAST-001) criticality benchmark while maintaining ENDF/B-VII.0 as the reference (or base) library for all other isotopes within the benchmark. A positively skewed keff distribution is observed in Fig. 2 (right). The non-Gaussian distribution observed is due to the tail of the relatively high calculated keff values obtained for the given benchmark. The high keff values give an indication that the current lead cross sections have some inaccuracies, which could result in more neutron reflection than is warranted by the experimental results. Furthermore, this could have implications for reactor safety.
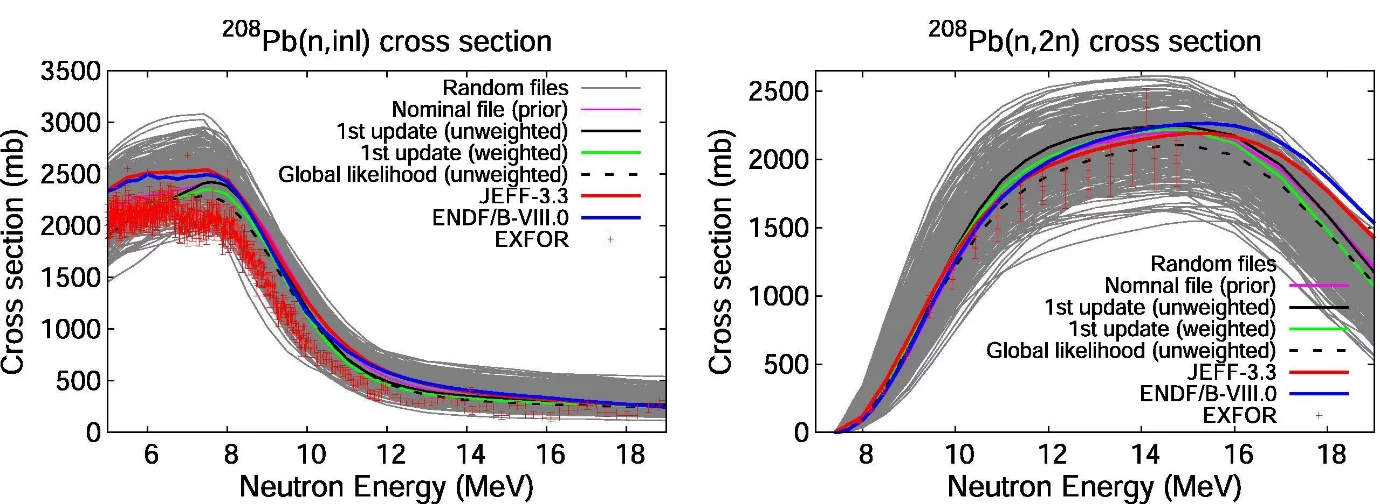
A final test of an adjustment is to compare the adjusted file back with differential experimental data (also known as differential validation) as well as with relevant benchmarks (if available) in order to determine the file’s performance. In Fig. 3, we compare the evaluation from this work in the case of the 208Pb(n,inl) and 208Pb(n,2n) cross sections, with differential experiments as well as with evaluations from other nuclear data libraries (JEFF-3.3 and ENDF/B-VIII.0). The results show that, our evaluation (i.e. the Global likelihood (unweighted)) is a better description of the experimental data compared with the other libraries, signifying that, there is a potential for the improvement of nuclear data evaluations through the combined use of differential and integral experimental data.
Contact
Dr. Alexander Vasiliev
Steady-State, Transient and Radiation Safety Analyses - System Group (STARS)
Laboratory for Reactor Physics and Thermal-Hydraulics (LRT)
Nuclear Energy and Safety Research Division (NES)
Paul Scherrer Institut
Original Publications
E. Alhassan, D. Rochman, H. Sjöstrand, A. Vasiliev, A.J. Koning, H. Ferroukhi
Bayesian updating for data adjustments and multi-level uncertainty propagation within Total Monte Carlo
Annals of Nuclear Energy 139 (2020)