Muonic atoms

Muonic atoms are atomic hydrogen-like bound states formed by a negative muon and a nucleus. The muon, which is the 200 times heavier cousin of the electron, orbits the nucleus with a 200 times smaller Bohr radius. This enhances the sensitivity of the atomic energy levels to the nuclear structure tremendously, in particular to the nuclear charge radius.

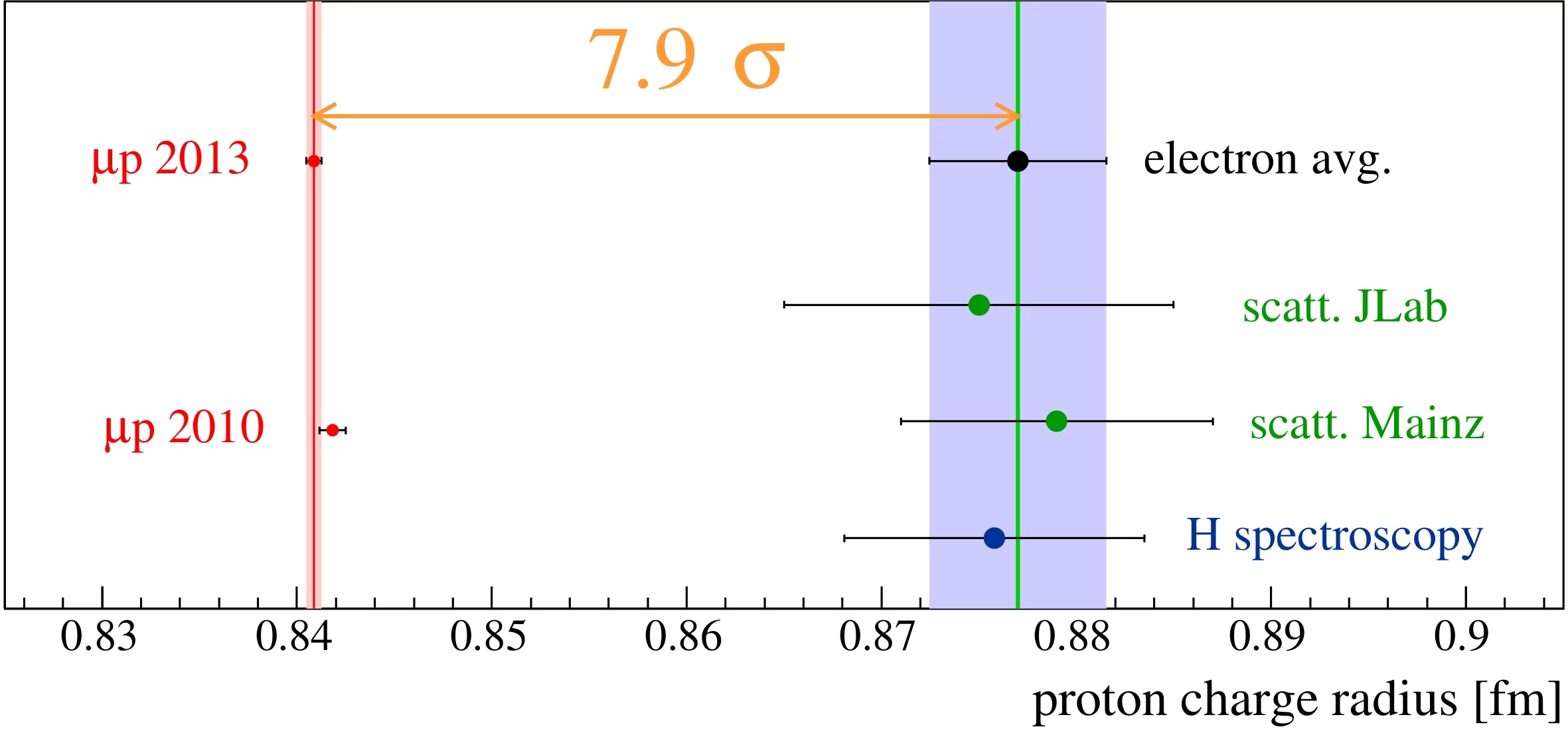
By measuring the 2S-2P energy difference in muonic hydrogen (μp) by means of laser spectroscopy with an accuracy of 10 ppm, we have determined the proton root mean square charge radius r_p = 0.84087(39) fm [1,2]. Its value is 20 times more precise than previously obtained. Yet, this value disagrees by 4 standard deviations from the value extracted from “regular” hydrogen spectroscopy [3,4] and also by 6 standard deviations from electron-proton scattering data [5,6,7] giving rise to a total discrepancy with "electronic" systems of about 8 standard deviations.

The variance of the various proton radius values has led to a very lively discussion [8] in various fields of physics: in particle and nuclear physics (proton structure, new physics, scattering analysis [9]), atomic physics (hydrogen energy level theory, fundamental constants) and fundamental theories (bound-state problems, QED, effective field theories). At present, however, the resolution to the problem remains unknown. Therefore several experiments are currently under way with the aim to check and improve the accuracy of the measurements in hydrogen [10,11,12,13] and in electron-proton scattering [14,15]. Moreover, muon-proton scattering has been proposed [16] to test possible deviations from the muon/electron universality.

An important piece of information regarding the “proton radius puzzle” is provided by spectroscopy of muonic deuterium (μd) and muonic helium ions (μ⁴He⁺, μ³He⁺) [17]. Measurements of two transition frequencies in μd and 5 in μHe⁺ have already been accomplished and data analysis is ongoing. The radii extracted from those measurements can be compared with already existing precise values from electron scattering [18].

Besides providing important information towards the resolution of the proton radius puzzle, these radii represent interesting and precise parameters to check few-nucleon ab-initio calculations, effective field nuclear theories, and nuclear potentials. These radii can be used to disentangle the 4 sigma discrepancy between two ⁴He-³He isotopic shifts measurements [19,20], and to provide absolute radii for ⁶He and ⁸He halo nuclei when combined with the corresponding isotopic shifts measurements [21]. Moreover their knowledge opens the way to enhanced bound-state QED tests for one- and two-electrons systems from measurements in ``regular'' He⁺ [22] and He [23, 24] based on XUV frequency comb techniques.

[1] R. Pohl et al., Nature 466, 213 (2010).
[2] A. Antognini et al., Science 339, 417 (2013).
[3] C.G. Parthey et al., Phys. Rev. Lett. 107, 203001 (2011).
[4] F. de Beauvoir et al., Phys. Rev. Lett. 78, 440 (1997).
[5] I. Sick, Phys. Lett. B 576, 62 (2003).
[6] J. C. Bernauer et al., Phys. Rev. Lett. 105, 242001 (2010).
[7] G. Lee, J.R. Arrington, R.J. Hill arXiv:1505.0148 9
[8] R. Pohl, R. Gilman, G.A. Miller, K. Pachucki, Annu. Rev. Nucl. Part. Sci 63, 165 (2013).
[9] I. T. Lorenz and U. G. Meiner, Phys. Lett. B 737, 57 (2014).
[10] A. Vutha et al., Talk: BAPS.2012.DAMOP.D1.138, 2012.
[11] A. Beyer, et al., Ann. Phys. 525, 671 (2013).
[12] 1S-3S transition at LKB, Paris.
[13] 1S-3S transition at MPQ, Garching.
[14] A. Gasparian [PRad at JLab Collaboration], EPJ Web Conf. 73, 07006 (2014).
[15] M. Mihovilovic et al. [A1 Collaboration], EPJ Web Conf.72, 00017 (2014).
[16] R. Gilman et al. [MUSE Collaboration], arXiv:1303.2160
[17] A. Antognini et al., Can. J. Phys. 89, 47 (2011).
[18] I. Sick, Phys Rev C 77, 941392(R) (2008).
[19] R. van Rooij et al. Science 333, 196 (2011).
[20] C. Pastor et al., PRL 108, 143001 (2012).
[21] Z.T. Lu, P. Mueller, G.W.F. Drake et al., Rev. Mod. Phys. 85, 1383 (2013).
[22] M. Herrmann et al., Phys. Rev. A 79, 052505 (2009).
[23] D.Z. Kandula et al., Phys. Rev. A 84, 062512 (2011).
[24] R. Notermans et al., PRA 90, 052508 (2014).